Crunchzilla – game maven
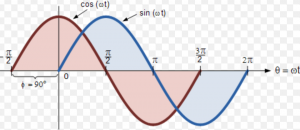
Calculate phase shift between two sine waves
Simulating wireless communication systems
C++ code available at Safari Books Online.
(Including PLL examples)
By: C. Britton Rorabaugh
http://my.safaribooksonline.com/book/electrical-engineering/communications-engineering/9780132442121
local code is in tkzic/simulating wireless dsp c++
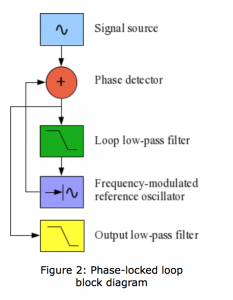
Understanding phase-locked loops
A nice explanation – with Python simulation.
By P. Lutus at arachnoid.com
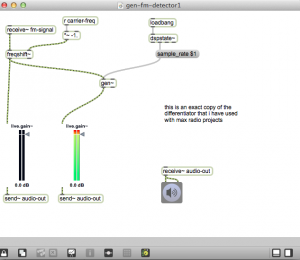
gen~ version of FM detector (differentiator)
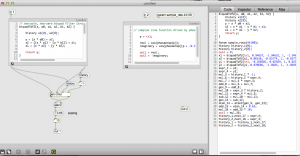
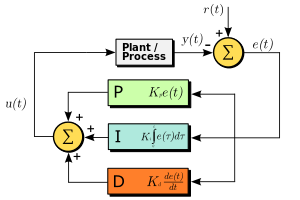
PID controller in Max
Here is a PID controller (proportional, integral, derivative) in Max that controls the pitch of an oscillator so you can watch how a process responds to various setting of PID coefficients. It features an external perturbance generator (ie., noise maker) to check how fast the system can adjust and continue.
Tried using fiddle~ for frequency detection (as the sensor input) but it provides faulty data below about 200hz – and that totally messes up the PID. so I am just using the actually frequency being used to set the oscillator as the response sensor.
update: Tristan Jehan wrote a Max external that extends lower frequency range of [fiddle~]. It would be worth trying for this patch.
The PID algorithm is written in javascript.
download
https://github.com/tkzic/max-projects
folder: pid-controller
patch: pid-mrmapes2.maxpat
javascript code: pid.js
Instructions
- turn on audio
- change test interval to something like 20
- click on message boxes to change set point. Listen and watch results
- try different presets – which alter PID settings and then try changing the set point. For example, with the 2nd preset you will see overshoot and oscillation during settling phase.
more about PID controllers
wikipedia page: http://en.wikipedia.org/wiki/PID_controller
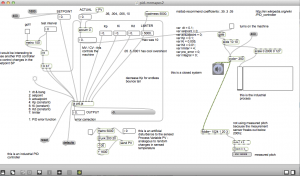
Phase locked loop FM detection in Max
Here is an example of audio from the patch.
The source is a speech by Barack Obama which is FM modulated on an audio carrier at 23040 Hz. Warning turn down the volume. You can hear as the PLL locks on to the signal. Then some of the params are tweaked in such a way that it is impossible to lock on to the signal, but the algorithm keeps on trying – producing an interesting result
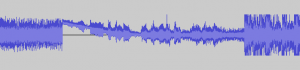
A picture of the signal as its locking-on and when it loses the lock:
[original post]
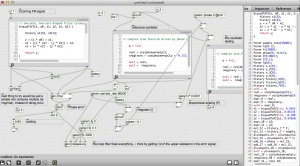
A phase-locked loop algorithm running in Max (gen~)
The patch is unstable – but actually demodulates FM now.
download
in max-projects: https://github.com/tkzic/max-projects
folder: demodulation/max/phase-locked-loop
patch
gen-fm-detector2.maxpat
(also uses output from modem3.maxpat in folder: demodulation/max/)
instructions
- run modem3.maxpat
- set FM modulation level to less than 250
- run gen-fm-detector2.maxpat
- turn up audio output and try presets
notes
Two things: 1) I really don’t know what I’m doing with gen~ and 2) There are serious issues with the P and I coefficients in the algorithm. There is no ‘D’ coefficient yet – nor do I know whether its needed.
The thing that finally got it working was the loop filter component – which cleans up the output of the phase detector. The phase detector is essentially a phase ring modulator which contains not only the error signal, but also the sum of the incoming carrier and the reference oscillator. So the low pass filter gets rid of the high frequency component. By setting the resonance and cutoff extremely low, you can make the PLL start going a bit crazy in a beautiful way, lots of motion and spectral shifting.
Need to go through and analyze the output of the various stages, now to get the coefficients set properly – also, may need some kind of AGC on the input stage. Its very sensitive to over modulation and will distort badly.
Its interesting to play with the coefficients and hear the difference in how the demodulation works. By slowing down the P coefficient it not only slows lock response, but during lock, the output is muffled – so the P coefficient acts as a low pass filter – because it changes how responsive the circuit is in detecting changes in the input signal frequency (i.e., modulation).
There’s a weird thing going on – a fixed carrier is getting mixed with the error signal (output) The patch is using notch filters to eliminate it, but it seems like it shouldn’t be there at all. Or should get filtered by the Loop filter.
Another thing to mention if I haven’t already is that I’m using a somewhat inefficient way to detect phase difference. Its the convert to complex and slope detection method used in the differentiator – but done using signals from reference oscillator instead of from delayed samples from original signal. Simply multiplying the two signals without complex conversion would probably do.
gen~ biquad patches
These algorithms were used for PLL FM detection. Details here: https://reactivemusic.net/?p=8253
original post
The lowpass at the end of this thread sets the biquad coefficients http://cycling74.com/forums/topic/codebox-qeustion/
And this is the actual biquad http://cycling74.com/forums/topic/genbiquad/
Columbia course notes g6611 gen~ links
At Columbia Unversity computer music.
http://music.columbia.edu/cmc/courses/g6611/spring2012/week7/index.html