Tag: math

Posted on

12th root of 2

The note relationships in a chromatic scale are based on the 12th root of 2.

An octave has a ratio of 2. An octave is divided into 12 equal steps.

For example, to find the ratio of one semi-tone (half step), on a scientific calculator, use this button:

Screen Shot 2015-03-23 at 12.36.27 PM

Here’s the result where x = 2 and y = 12

Screen Shot 2015-03-23 at 12.47.48 PM

In a computer program, you could use the pow() function calculate 2 to the 1/12 power. Here’s an example in javascript:

Screen Shot 2015-03-23 at 12.44.03 PM

This Max patch shows the relationships between any two notes and how to calculate the pitch of a note based on the semi-tone interval. You might use it as a starting point to design your own scales. For example, a 13 note chromatic scale.  Or relationships based on randomness.

Screen Shot 2015-03-23 at 12.32.36 PM

Download

https://github.com/tkzic/max-projects 

folder: 12throotof2

patch: 12throotof2.maxpat

Posted on

Phasor

Engine of time.

from Wikipedia

http://en.wikipedia.org/wiki/Phasor

Unfasor

 

Traveling along the outer edge of the circle, the distance goes from 0 to 2*PI radians, then starts over again. In degrees it would be 0 to 360. A clock goes from 0 to 12. In Max and Pd the phasor~ objects are normalized to run from 0.0 to 1.0. Think of flattening out the edge of the circle to a straight line.

The phasor as input to a sine or cosine function generates one  cycle of a wave for each revolution – as shown in the above animation. For example, cosine would go from 0 to 1 to 0 to -1 to 0.

If you graph the phasor value, it looks like a sawtooth wave – rising in a ramp from 0.0 to 1.0 then falling straight down to 0.0 to start again.

With waves, the distance around the circle represents time (or phase), the projected cosine value represents amplitude.

In science…

“A phasor can be considered a vector rotating about the origin in a complex plane. The cosine function is the projection of the vector onto the real axis. Its amplitude is the modulus of the vector, and its argument is the total phase 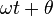\omega t+\theta. The phase constant \thetarepresents the angle that the vector forms with the real axis at t = 0.”

-WIkipedia

In art…

“And the seasons they go round and round 
And the painted ponies go up and down 
We’re captive on the carousel of time 
We can’t return we can only look 
Behind from where we came 
And go round and round and round 
In the circle game.”

-Joni Mitchell

(These lyrics happen at about 4:40 in the video…)